| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 깃
- 엑셀
- matlab
- 비주얼베이직
- Windows11
- Windows10
- 파이썬GUI
- 오피스
- pyqt5
- 파워포인트
- 안드로이드
- windows
- pythongui
- Outlook
- 윈도우10
- VBA
- 윈도우11
- Android
- 아웃룩
- 파이썬
- git
- html
- python
- pandas
- 파이썬3
- win32com
- Excel
- 문자열
- office
- python3
Appia의 IT세상
파이썬 [Python] 016 최대 공약수 최소 공배수 구하기, 유클리드 호제법 본문
오늘은 최대 공약수 최소 공배수를 구하는 연산을 구하고자 합니다. 오늘 주변에 아시는 분께서 갑자기 저에게 최소 공배수, 최대 공약수 문제를 면접 시험 문제로 낸다고 문제와 코드를 주라고 해서 부랴부랴 작성을 하게 되었습니다. 실제로, 너무 오래되서 그런지 이제 어떻게 구현하는데 조차 기억이 좀 가물가물 하는데요. 오늘은 이 최대 공약수와 최소 공배수 구하를 방법에 대해서 살펴보도록 하겠습니다.
최대공약수 - 0이 아닌 두 정수나 다항식의 공통되는 약수중에서 가장 큰수
최소 공배수 - 두 정수가 공통적으로 가지는 배수중 가장 작은 것
일단 간단히 한번 최대 공약수를 구해보도록 하겠습니다. 두 정수 예를 들면 60, 44를 2란 정수로 나누어 보도록 하겠습니다. 몫으로 30, 22가 나옵니다. 다시 이를 2로 나누어 보도록 하겠습니다. 그럼 15, 11이 나옵니다. 15와 11은 실제 나누어 지는 정수가 없으므로, 최대 공약수는 4가 됩니다. 여기서 각각 나눌 때 사용한 수를 곱하여 최대 공약수를 구할 수 있습니다. 여기서 최소 공배수는 최대 공약수 * 11 * 15입니다.
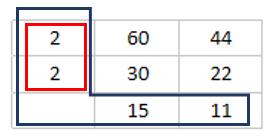
< 최대 공약수 구하기>
그럼 관련해서 코드로 작성을 해볼까 합니다. 그전에 어떻게 코드를 작성할 것인지에 대해서 한번 생각해보도록 하겠습니다.
저의 경우 일단 약수를 구하는 방식으로 최대 공약수를 추출하고자 합니다.
1. 약수를 저장할 수 있는 리스트 형을 하나 만듭니다.
2. 그런 후 두 정수 중 작은 수를 기반으로 반복문을 구성합니다. 즉, 1 부터 작은 수까지 반복하는 반복문입니다. 그안에서는 즉, 1부터 시작해서 두 정수를 나누어 나머지가 0인 수들을 리스트형에 모두 저장할 것입니다.
3. 그런 후에 반복문이 종료 되면, 가장 큰 약수만 출력하는 형태로 사용하고자 합니다. 그럼 한번 코드로 살펴보겠습니다.
def gcd(A,B):
ListV = []
if A > B :
targetV = B
else :
targetV = A
for i in range(1, targetV+1):
if A%i == 0 and B %i == 0:
ListV.append(i)
var = max(ListV)
return var,ListV
V, ListT = gcd(60,44)
print(ListT) # 모든 약수 출력
print(V) # 최대 공약수 출력
다음 최소 공배수에서 다시 한번 활용하기 위해서 함수 형태로 정의 하여 사용하였습니다. 위의 코드를 실행하면 다음과 같은 결과가 나올 것입니다.
[1, 2, 4]
4
<최소 공배수 구하기>
위에서 생성된 최대 공약수로 각 정수를 나누어 몫을 구합니다.
그리고 나서 최대공약수와 각 몫을 곱하여 최소 공배수를 구합니다.
그럼 코드로 한번 살펴보도록 하겠습니다.
def lcm(A,B):
V, ListT = gcd(A,B) # 앞서 예시에서 선언한 함수 재사용 최대 공약수 재실행
divA = A//V
divB = B//V
return V * divA * divB
print(lcm(60, 44))
위의 코드를 실행하면 다음과 같은 결과가 나옵니다.
660
<유클리드 호제법>
그럼 이제 다른 형태로 한번 구해보고자 합니다. 앞서서 최소 공배수, 최대 공약수를 구했는데, 조금 더 쉽게 구하는 방법이 있습니다. 바로 중학교 때 배웠던 유클리드 호제법입니다.. 즉 2개의 자연수의 최대 공약수를 구하는 알고리즘의 하나입니다.
두 정수 a,b에 대해서 a>b일 때, a=bq+r이라 하면 gcd(a,b) = gcd(b,r)이다. (단 0<=r)
위의 글을 좀더 쉽게 풀어서 이야기 하면, a를 b의 최대공약수는 a를 b로 나눌 때 생기는 나머지 c 와 b의 최대 공약수와 같다는 사실입니다.
간단하게 48과 21로 예를 들어보겠습니다.
먼저 48를 21로 나누면 나머지가 6입니다.
그러면 21을 6으로 나눈 나머지는 3입니다.
6을 3으로 나누며 나머지가 0입니다.
즉 3이 이 48과 21의 최대 공약약수가 됩니다.
그럼 관련해서 코드로 작성해 보겠습니다.
def uclid_gcd(A,B):
if A>B :
Target = A
SubTarget = B
else :
Target = B
SubTarget = A
Remaining = Target % SubTarget
if Remaining != 0:
return uclid_gcd(SubTarget,Remaining)
else :
return SubTarget
print(uclid_gcd(48,21))
위의 코드에서 시작부에서는 무조건 큰수를 비교하는 형태로 넣었습니다. 꼭 코딩을 하다보면, 이런 부분에서 문제가 나기 쉽기 때문이죠. 유클리드 호제법에서는 무조건 A>B조건이지만, 혹 실수로 잘못 넣을 수 있음을 대비하였습니다. 또한 재귀 함수를 이용했습니다.
위의 코드를 실행하면 다음과 같은 결과를 얻을 수 있습니다.
3
오늘은 최대 공약수, 최소 공배수, 그리고 유클리드 호제법을 이용한 최대 공약수 구하는 방법에 대해서 살펴보았습니다.저는 실제 코딩을 함에 있어서 정답을 없다고 생각합니다. 각자 코드를 작성하는 자가 원하는 답을 얻었을 때 그 코드는 정답인 코드라고 생각합니다. 그래서 보이는 부분이 때론 많이 부족할 수 있지만, 그럴 경우 댓글로 코맨트 부탁드립니다. 혹, 다른 문의 사항 및 궁금한 사항이 있으시면 언제든지 댓글 부탁드립니다. 감사합니다.
'Python > Python 응용' 카테고리의 다른 글
| 파이썬 [Python] 018 win32com 이용 Excel파일 CSV파일로 저장하기 (0) | 2019.12.29 |
|---|---|
| 파이썬 [Python] 017 win32com 이용하여 Excel 제어하기 (2) | 2019.12.29 |
| 파이썬 [Python] 015 진법 변환 (10진수, 2진수, 8진수, 16진수 변환) (0) | 2019.12.28 |
| 파이썬[Python] 014 Pywin32 설치 (0) | 2019.12.28 |
| 파이썬[Python] 013 로또(lotto) 번호 생성기 만들기와 random 모듈 (0) | 2019.12.28 |



